Temas de Álgebra Superior

UNIVERSIDAD HIPÓCRATES

LICENCIATURA EN MATEMÁTICAS

ÁLGEBRA SUPERIOR

 DOCENTE: ING. OLGA MARÍA TESTA RODRÍGUEZ.

TEMAS DE ÁLGEBRA SUPERIOR

ALUMNO: IVÁN EMILIO SALGADO OJEDA.

GRUPO: LAM 2

ÍNDICE

 
 1.-ÁLGEBRA

• Definición
• Álgebra superior

2.-CONCEPTOS PRELIMINARES

• Conjuntos
• Operaciones entre conjuntos
• Números imaginarios
• Clasificación de los números

3.-RELACIÓN

• Definición 
• Tipos de relación
• Ejemplos

4.-FUNCIONES

• Definición
• Tipos de funciones
• Ejemplos
• Dominio y Codominio de una función
• Ejemplos del dominio y recorrido con funciones

5.-COMBINACIONES Y PERMUTACIONES

• Definición
• Ejemplos

6.-ÁLGEBRA MATRICIAL

• Definición
• Tipos de matrices
• Operaciones con matrices
• Ejemplos de operaciones con matrices

7.-FORO DE DISCUSIÓN

8.-REFERENCIAS




Definición de álgebra

El álgebra es la rama de la matemática que estudia la combinación de elementos de estructuras abstractas acorde a ciertas reglas. Estos elementos podían ser interpretados como números o cantidades, por lo que el álgebra en cierto modo originalmente fue una generalización y extensión de la aritmética.

El álgebra conforma una de las grandes áreas de las matemáticas. A diferencia de la aritmética elemental, que trata de los números y las operaciones fundamentales, en álgebra para lograr la generalización- se introducen además símbolos (usualmente letras) para representar parámetros (variables o coeficientes), o cantidades des conocidas (incógnitas); las expresiones así formadas son llamadas "fórmulas algebraicas", y expresan una regla o un principio general.

Álgebra Superior

El conocimiento de álgebra superior es indispensable para la formación matemática. Como principio, en cuanto a los temas que se desarrollan en esta materia se encuentran los conjuntos y en especial los conjuntos numéricos.
En álgebra superior se presentan los métodos generales de análisis y resolución de sistemas de ecuaciones, así como los conceptos fundamentales de la teoría de ecuaciones.

El álgebra superior es una combinación de tres disciplinas:

• Álgebra lineal
• Álgebra abstracta
• Topología general y algebraica

 Conceptos preliminares

 Conjunto: Es un grupo formado por una determinada cantidad de elementos que tienen alguna característica en común.

Operaciones entre conjuntos 

Las operaciones que se pueden realizar entre conjuntos son:

Unión

La  unión de los conjuntos  A y  B es el conjunto de todos los elementos de  A con todos los  elementos de  B sin repetir ninguno y se denota como  A∪ B . Esto es:

Intersección

La  intersección de los conjuntos  A y  B es el conjunto de los elementos de  A que también  pertenecen a  B y se denota como  A∩ B . Esto es:

Dos conjuntos son ajenos o disjuntos cuando su intersección es el conjunto vacío, es decir, que no tienen  nada en común. Por ejemplo:

Complemento

El complemento del conjunto  A con respecto al conjunto universal  U es el conjunto de todos los  elementos de U que no están en  A y se denota como  'A . Esto es:

Diferencia

La  diferencia de los conjuntos  A y  B (en ese orden) es el conjunto de los elementos que pertenecen a  A y no pertenecen a  B y se denota como  A− B . Esto es:

Números Imaginarios

En matemáticas un número imaginario es un número complejo (compuesto por dos dígitos) cuya parte real es igual a cero.

Por ejemplo:

5i es un número imaginario, así como i ó -i son también números imaginarios.

En otras palabras, es un número de la forma:

z = x + yi  : x = 0

Un número imaginario puede describirse como el producto de un número real por la unidad imaginaria "i", en donde "i" denota la raíz cuadrada de -1.

Clasificación de los números

 

Relaciones

Definición:

Sea A y B conjuntos, una relación entre A y B es un subconjunto del producto cartesiano A x B.

Ejemplo:

       Si A = {a}  y B = {b}

Entonces A x B = {(a,b)} y existen 2 relaciones entre A y B, la vacía y la total.

Ejemplo 2:

Relación entre polígonos y su número de lados a partir de 2 conjuntos denotados A y B.

Clasificación de relaciones

• Relaciones de equivalencia
• Relaciones de orden
• Funciones

Relaciones de equivalencia 

Características (propiedades)

1) Reflexividad: xRx : ∀x ∈ S ⇒ xRx
( x está relacionada con x )

Ejemplo: El conjunto de alumnos que se encuentra en su salón de clase

S = {Pedro, Javier, Esteban}

R : está en la misma habitación

Pedro R Pedro → reflexividad

2) Simetría: ∀x, y ∈ S . Si x Ry ⇒ yRx

Ejemplo: Pedro R Javier ⇒ Javier R Pedro 

3) Transitiva: ∀x, y,z ∈ S Si xRy y yRz ⇒ xRz

Pedro R Javier y Javier R Esteban ⇒ Pedro R Esteban

Definición: 
Una relación R , definida sobre un conjunto S es una relación de equivalencia ⇔
tienen las tres propiedades: reflexiva, simétrica y transitiva.

 

 Relación de orden parcial

 En matemáticas, una relación binaria R sobre un conjunto X es antisimétrica si se cumple que para todo a y b pertenecientes a X si a está relacionado con b y b está relacionado con a entonces a = b.

Ejemplo: A= {12,6,4,3,21} conjunto de divisores positivos enteros de 12 →xRy x divide exactamente a y. 

Funciones

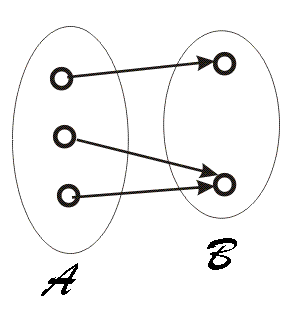
Intuitivamente una función es una regla que asocia elementos de un conjunto A con elementos de un conjunto B de modo que el elemento del conjunto A se asocia con uno y sólo un elemento del segundo conjunto.

Definición: 

Sean A y B dos conjuntos. Una función de A en B es un conjunto de pares ordenadas de A x B (a, b) con la propiedad de que cada elemento de A es el primer componente de una pareja ordenada y para todo a ∈ A, si  (a, b) y (a, c) pertenece a f entonces b = c (porque a no se repite en otra pareja). 

A: Dominio de la función
 B: Codominio   

Ejemplo: A= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} = {conjunto de calificaciones en base a 10}  

DOMINIO Y CODOMINIO DE UNA FUNCIÓN

 Dominio de una función:
 Es el conjunto de los valores que puede tomar x o que toma x para que exista la función. 

Codominio o rango de una función:
 Es el conjunto de los valores que se obtienen al sustituir los valores del dominio en la función. 

TIPOS DE FUNCIONES 

 

Función Inyectiva: A una función en la que a cualquiera par de elementos diferentes del dominio les corresponde imágenes diferentes se le llama función inyectiva (significa uno a uno).

 

Un ejemplo de función inyectiva es la siguiente función cuadrática:

 

Función Suprayectiva: Si todo elemento del codominio de una función f es imagen de al menos un elemento de su dominio, entonces f es una función suprayectiva.

Las funciones trigonométrica (seno, coseno, tangente, cotangente, secante y cosecante) son del tipo suprayectiva (o sobreyectiva). El dominio son los reales y el codominio es [-1, 1] por lo que para más de un valor de x le corresponde el mismo valor de y.   

 Ejemplo:

Función Biyectiva: Una función que es suprayectiva  e inyectiva se llama Biyectiva. 

Ejemplo de esta función es la siguiente función lineal: 

Cuyo dominio y cuyo codominio son los reales. Para cada valor de x le corresponde solo uno de y. Todos los valores del codominio son la imagen de un valor y solo uno del dominio.  

 

Combinaciones y permutaciones

Definiciones:

En matemáticas usamos un lenguaje más preciso:

	Si el orden no importa, es una combinación.
	Si el orden sí importa es una permutación.

Permutaciones

Hay dos tipos de permutaciones:

1. Se permite repetir: como la cerradura de un candado, podría ser "333".
2. Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.

Combinaciones

También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):

1. Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
2. Sin repetición: como números de lotería (2,14,15,27,30,33)

 ÁLGEBRA MATRICIAL

 MATRICES Y DETERMINANTES

 Introducción
Las matrices y los determinantes son herramientas del álgebra que facilitan el ordenamiento de datos, así como su manejo.

Las matrices se encuentran en aquellos ámbitos en los que se trabaja con datos regularmente ordenados y aparecen en situaciones propias de las Ciencias Sociales , Económicas y Biológicas.

Matrices

Definición y primeros ejemplos
Una matriz es una tabla rectangular de números reales dispuestos en filas y columnas del modo:

Son ejemplos de matrices los siguientes:

Tipos de matrices

Matriz Nula

Se llama matriz nula a la que tiene todos los elementos cero.

Por ejemplo:

A = (00000

        00000)

Es una matriz nula de tamaño 2x5.

Matriz Fila

Se llama matriz fila a la que solo tiene una fila, es decir su dimensión es 1x n.
Por ejemplo:

                                     B= (1  0  4 9)

Es una matriz fila de tamaño 1 x 4.

Matriz Columna

 Se llama matriz columna a la que sólo consta de una columna, es decir su dimensión será m x 1
 Por ejemplo:

Es una matriz columna de tamaño 4x 1.

Matriz Cuadrada

Una matriz es cuadrada cuando tiene el mismo número de filas que de columnas, es decir su dimensiones n x n. 

Un ejemplo de matriz cuadrada es:

 

 Matriz cuadrada de orden 3. 

Diagonales en una Matriz

En las matrices cuadradas podemos encontrar 2 tipos de diagonales, una primaria y una secundaria.

Ejemplo:

 

Operaciones con matrices

 Suma y diferencia

 Dadas dos matrices A y B podemos realizar su suma o diferencia de acuerdo a la siguiente regla: 

Para sumar o restar dos matrices del mismo tamaño, se suman o restan los elementos que se encuentren en la misma posición, resultando otra matriz de igual tamaño. 

Por ejemplo:

  

Si las matrices tienen diferente tamaño, no se pueden sumar o restar entre sí.

Trasposición de matrices

 Dada una matriz cualquiera A, se llama matriz traspuesta de A, y se representa por At a la matriz que resulta de intercambiar las filas y las columnas de A.

Por ejemplo:

Multiplicación de Matrices

 
Hay que dejar claro ya desde el principio que no todas las matrices pueden multiplicarse. Dos matrices se pueden multiplicar cuando se cumple la siguiente condición:

“Para multiplicar dos matrices A y B, en este orden, A ·B , es condición indispensable que el número de columnas de A sea igual al número de filas de B”

 Si no se cumple esta condición, el producto A ·B no puede realizarse, de modo que esta es una condición que debemos comprobar previamente a la propia multiplicación.

 Una vez comprobado que el producto A·B se puede realizar, si A es una matriz m x n y B es una matriz n x p (observemos que el n º de columnas de A = n = nº de filas de B), entonces el producto A·B da como resultado una matriz C de tamaño n x p.

Ejemplo de multiplicación de matrices:

 A continuación les dejaré un video explicativo del proceso de multiplicación de matrices:

 

Propiedades del producto de matrices

 a) Asociativa: A·(B·C) = (A·B)·C.

b) Distributiva respecto de la suma: A·(B +C)=A·B + A·C (B +C)·A = B ·A+ C ·A.

c) Elemento neutro, la matriz identidad correpondiente, si A es m x n: A·In = A Im ·A = A.

 

d) En general el producto de matrices no es conmutativo A·B = B ·A.

e) El producto de dos matrices no nulas A y B puede dar lugar a una matriz nula.

  f) Se dice que el conjunto de las matrices con la operación producto tiene divisores de cero, es decir, hay matrices no nulas cuyo producto es nulo.
 

Foro de discusión

¿Para que sirven y en donde se aplican las matrices?

 

Referencias

Aurelio Baldor, Álgebra, pp. 5-6.

Roshdi Rashed (Noviembre 2009). Saqi Books. ed. Al Khwarizmi: The Beginnings of Algebra.

http://pendientedemigracion.ucm.es/info/pslogica/teoriaconjuntos.pdf

http://campus.cva.itesm.mx/nazira/Tc1003/PDF/Apuntes/0400Tc1003_Relaciones_funciones.pdf

www.amatematicas.cl/sw.a/00001192